Estructuras de control: Secuencial, selección e iteración

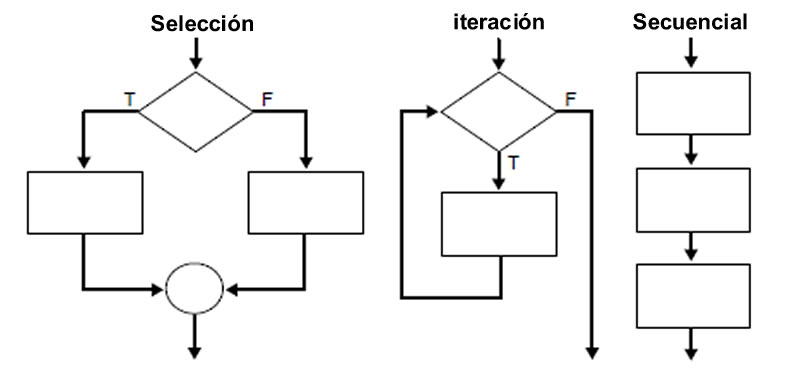
El teorema de la programación estructurada describe tres estructuras básicas de control con las que demuestra que es posible resolver cualquier problema computacional.

Estructura secuencial

Haremos un breve repaso para recordar que la estructura secuencial consiste en ejecutar, secuencialmente, una acción simple detrás de otra.

Recordemos, también, que se considera acción simple a las acciones de leer, escribir, asignar valor a una variable e invocar a un módulo o función.

Estructura de decisión

La estructura de decisión permite decidir entre ejecutar uno u otro conjunto de acciones en función de que se cumpla o no una determinada condición lógica.

En el artículo anterior, explicamos el uso del if. Más adelante, en este mismo artículo, veremos que existen otras estructuras selectivas como por ejemplo la decisión múltiple (switch) y el if-inline.

Comencemos por analizar un problema extremadamente simple.

Problema 2.1

Leer dos valores numéricos enteros e indicar cuál es el mayor y cuál es el menor. Considerar que ambos valores son diferentes.

Análisis

Los datos de entrada para este problema son los dos valores que ingresará el usuario. Nuestra tarea será compararlos para determinar cuál es mayor y cuál es menor.

El enunciado dice que debemos considerar que los valores serán diferentes. Por lo tanto, para nuestro análisis la posibilidad de que los valores sean iguales no será tomada en cuenta.

Llamaremos a al primer valor y b al segundo. Para compararlos utilizaremos una estructura de decisión que nos permitirá determinar si a es mayor que b.

Si esto resulta verdadero, entonces a será el mayor y b será el menor. De lo contrario, si la condición anterior resulta falsa, b será el mayor y a el menor ya que, como mencionamos más arriba, a y b no serán iguales.

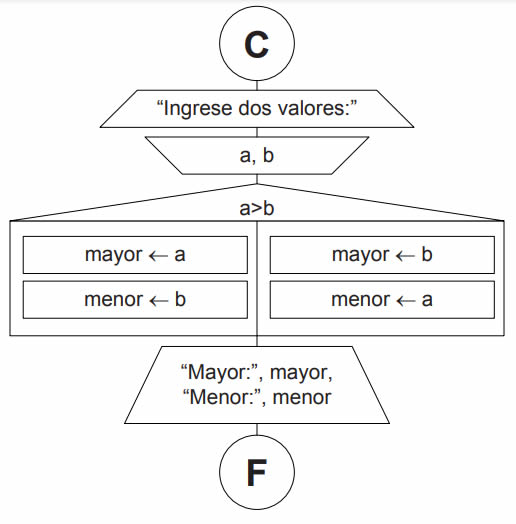
En el algoritmo utilizamos las variables mayor y menor. Una vez que comparamos a con b y determinamos cuál es el mayor y cuál es el menor, asignamos sus valores a estas variables y luego, mostramos sus contenidos.

El código fuente es el siguiente:

#include <stdio.h>
int main() {
	int a,b;
	int mayor,menor;

	printf("Ingrese dos valores: ");
	scanf("%d %d",&a,&b);

	if( a>b ) {
		mayor=a;
		menor=b;
	} else {
		mayor=b;
		menor=a;
	}

 	printf("Mayor: %d\n",mayor);
 	printf("Menor: %d\n",menor);
 	
 	system("pause");
 	return 0;
}

Para resolver este problema, utilizamos una estructura de decisión que nos permitió determinar cuál es el mayor valor. Luego, por descarte, el otro es el menor.

Estructuras de decisión anidadas

Cuando en una estructura de decisión utilizamos dentro otra estructura de decisión, decimos que ambas son estructuras anidadas.

En el siguiente problema, utilizaremos estructuras de decisión anidadas para determinar, entre tres valores numéricos, cuál es el mayor, cuál es el del medio y cuál es el menor.

Problema 2.2

Leer tres valores numéricos enteros, indicar cuál es el mayor, cuál es el del medio y cuál, el menor. Considerar que los tres valores serán diferentes.

Veamos primero el algoritmo y luego lo analizaremos.

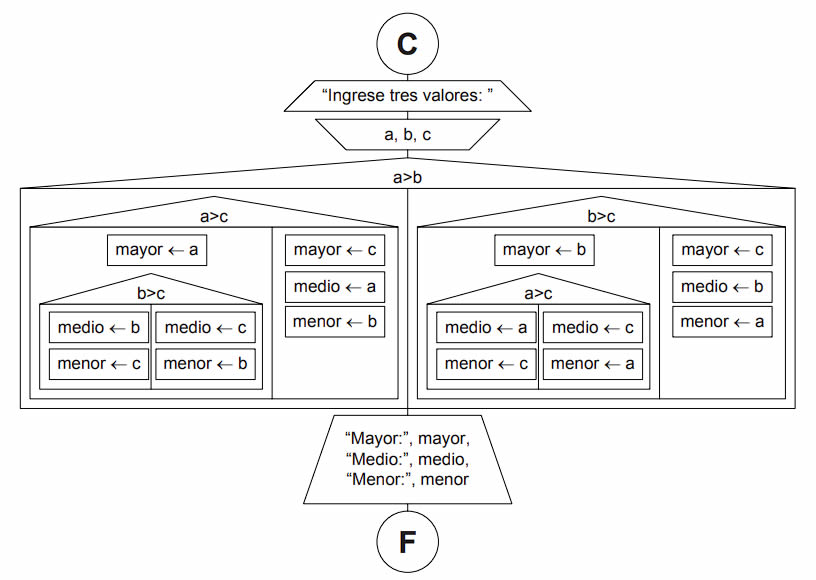
Análisis

Leemos los tres valores y comenzamos a comparar preguntando si a>b. Si esto se verifica entonces preguntamos si a>c. Si esto también se verifica entonces, como a>b y a>c, no hay dudas de que a es el mayor. Luego tenemos que comparar b y c para ver cuál está en segundo y en tercer lugar.

Si resulta que a>b pero no se verifica que a>c (es decir que c es mayor que a) será porque c es el mayor, a el medio y b el menor.

Por otro lado, si no se verifica que a>b preguntamos si b>c. Si esto es así, entonces el mayor será b (ya que b es mayor que a y b es mayor que c). Preguntamos si a>c y podremos deducir cuál está en segundo y tercer lugar.

Para finalizar, si es falso que b>c entonces el mayor será c, medio b y menor a.

El código fuente es el siguiente:

#include <stdio.h>
int main() {
	int a,b,c;
	int mayor,medio,menor;

	printf("Ingrese tres valores: ");
 	scanf("%d %d %d",&a,&b,&c);

 	if( a>b ){
		if( a>c ) {
	 		mayor=a;
	 		if( b>c ) {
	 			medio=b;
	 			menor=c;
	 		} else {
	 			medio=c;
	 			menor=b;
	 		}
	 	} else {
		 	mayor=c;
		 	medio=a;
		 	menor=b;
		}
	} else {
	 	if( b>c ) {
	 		mayor=b;
	 		if( a>c ) {
	 			medio=a;
	 			menor=c;
	 		} else {
	 			medio=c;
	 			menor=a;
	 		}
	 	} else {
 			mayor=c;
 			medio=b;
 			menor=a;
 		}
 	}

	printf("Mayor: %d\n",mayor);
	printf("Medio: %d\n",medio);
	printf("Menor: %d\n",menor);
	
	system("pause");
	return 0;
}

Para resolver este ejercicio recurrimos al uso de estructuras de decisión anidadas. El lector habrá notado que, a medida que anidamos más estructuras de decisión, resulta más complicado de seguir el código fuente.

Quizás un mejor análisis del problema hubiera sido el siguiente: Si a>b && a>c entonces el mayor es a, el del medio será el máximo valor entre b y c y el menor será el mínimo valor entre estos.

Si la condición anterior no se verifica será porque a no es el mayor valor.

Supongamos entonces que b>a && b>c. En este caso, el mayor será b y los valores medio y menor serán el máximo entre a y c y el mínimo entre a y c respectivamente.

Siguiendo este análisis, el algoritmo podría plantearse de la siguiente manera:

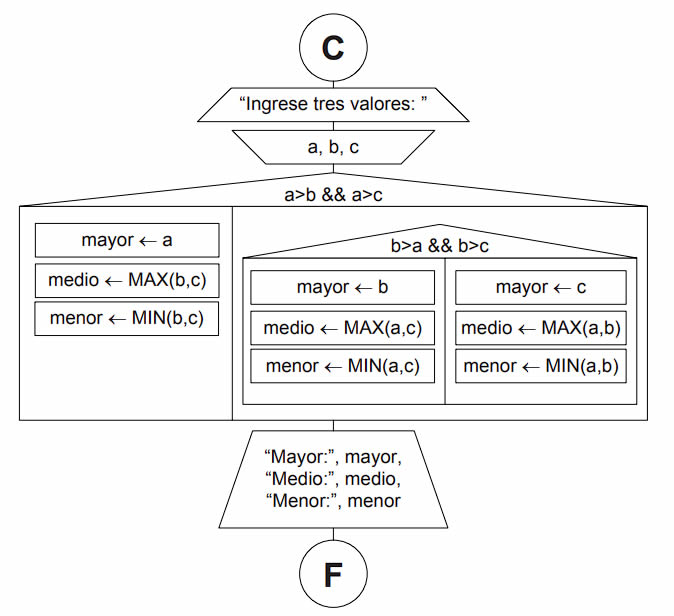
Para implementar esta solución, utilizaremos la estructura de selección en línea o if-inline.

Selección en línea o if-inline

Esta estructura implementa un if en una única línea de código y funciona así:

resultado = condicion ? expresion1:expresion2;

Si condicion resulta verdadera el if-inline retorna la expresión ubicada entre el signo de interrogación y los dos puntos. Si condicion resulta falsa entonces el valor de retorno será la expresión ubicada inmediatamente después de los dos puntos.

Por ejemplo: sean las variables a y b enteras y cada una con un valor numérico, y la variable mayor también entera, entonces:

mayor = a>b?a:b; // asigno a mayor el maximo valor entre a y b

Esta línea debe interpretarse de la siguiente manera:

Si se verifica que a>b entonces el if-inline retorna a (expresión ubicada entre el signo de interrogación y los dos puntos). Si la expresión lógica no se verifica entonces el valor de retorno del if-inline será b (expresión ubicada luego de los dos puntos). El resultado del if-inline lo asignamos a la variable mayor.

Utilizando el if-inline podemos codificar la segunda versión del problema 2.2 haciendo que sea más legible al reducir la cantidad de “ifes” anidados.

#include <stdio.h>
int main() {
	int a,b,c;
	int mayor,medio,menor;

	printf("Ingrese tres valores: ");
	scanf("%d %d %d",&a,&b,&c);

	if( a>b && a>c ) {
		mayor=a;
		medio=b>c?b:c; // el mayor entre b y c
		menor=b<c?b:c; // el menor entre b y c
	} else {
		if( b>a && b>c ) {
			mayor=b;
			medio=a>c?a:c; // el mayor entre a y c
			menor=a<c?a:c; // el menor entre a y c
		} else {
			mayor=c;
			medio=a>b?a:b; // el mayor entre a y b
			menor=a<b?a:b; // el menor entre a y c
		}
 	}

 	printf("Mayor: %d\n",mayor);
 	printf("Medio: %d\n",medio);
 	printf("Menor: %d\n",menor);
 	
 	system("pause");
 	return 0;
}

Macros

Las macros son directivas de preprocesador con las que podemos relacionar un nombre con una expresión.

Por ejemplo:

#define MAX(x,y) x>y?x:y
#define MIN(x,y) x<y?x:y

El preprocesador de C reemplazará cada macro por la expresión que representa. Así, podemos invocar a la macro MAX de la siguiente manera:

mayor = MAX(a,b);

donde a y b son argumentos que le pasamos a la macro MAX. El preprocesador reemplazará la línea anterior por la siguiente línea:

mayor = a>b?a:b

Utilizando estas macros podemos mejorar aún más la legibilidad del código del problema 2.2.

#include <stdio.h>
// definimos las macros
#define MAX(x,y) x>y?x:y
#define MIN(x,y) x<y?x:y
int main() {
	int a,b,c;
	int mayor,medio,menor;

	printf("Ingrese tres valores: ");
	scanf("%d %d %d",&a,&b,&c);

	if( a>b && a>c ) {
		mayor=a;
		medio=MAX(b,c);
		menor=MIN(b,c);
	 } else {
	 	if( b>a && b>c ) {
			mayor=b;
			medio=MAX(a,c);
			menor=MIN(a,c);
		} else {
 			mayor=c;
 			medio=MAX(a,b);
 			menor=MIN(a,b);
 		}
 	}

	printf("Mayor: %d\n",mayor);
	printf("Medio: %d\n",medio);
	printf("Menor: %d\n",menor);
	
	system("pause");
	return 0;
}

Selección múltiple (switch)

La estructura de selección múltiple permite tomar una decisión en función de que el valor de una variable o el resultado de una expresión numérica entera coincidan o no con alguno de los valores indicados en diferentes casos o con ninguno de estos. Gráficamente, la representaremos así:

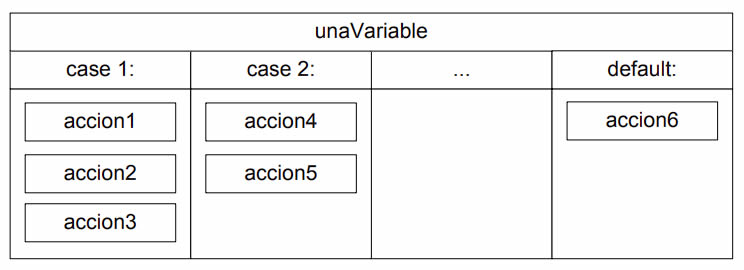
Este gráfico debe interpretarse de la siguiente manera: si el valor de unaVariable es 1 entonces se ejecutarán las acciones accion1, accion2 y accion3. En cambio, si unaVariable vale 2 se ejecutarán las acciones accion4 y accion5. Podemos agregar tantos casos como necesitemos. Por último, podemos indicar la opción default que representa a todos los otros casos que no fueron indicados explícitamente.

A continuación, vemos la sintaxis genérica de esta estructura.

switch(expresion) {
	case expresion_cte_1:
		sentencia_1;
		break;
	case expresion_cte_2:
		sentencia_2;
		break;
	.
	.
	.
	case expresion_cte_n:
		sentencia_n;
		break;
	[default:
		sentencia;]
}

Los casos deben representarse con valores numéricos literales o constantes. El caso default es opcional.

Problema 2.3

Leer un valor numérico que representa un día de la semana. Se pide mostrar por pantalla el nombre del día considerando que el lunes es el día 1, el martes es el día 2 y así, sucesivamente.

Análisis

Este problema se puede resolver fácilmente utilizando una estructura de selección múltiple como veremos a continuación:

En el diagrama leemos el número de día en la variable nroDia y luego, utilizamos una estructura de selección múltiple (switch) con los casos 1, 2, 3, 4, 5, 6 y 7.

Si el usuario ingresó el número de día 1, entonces la estructura ingresará por el caso case 1 donde le asignamos la cadena “Lunes” a la variable dia. Análogamente, si el usuario ingresa el valor 2, entraremos por case 2 y le asignaremos a dia la cadena “Martes” y así, sucesivamente.

La codificación es la siguiente:

#include <stdio.h>
#include <string.h>
int main() {
	int nroDia; char dia[10];
	printf("Ingrese dia de la semana: ");
	scanf("%d",&nroDia);

	switch( nroDia ) {
		case 1:
			strcpy(dia,"Lunes"); // asigno a dia la cadena "Lunes"
			break;
		case 2:
			strcpy(dia,"Martes"); // asigno a dia la cadena "Martes"
			break; 
		case 3:
			strcpy(dia,"Miercoles");
			break;
		case 4:
			strcpy(dia,"Jueves");
			break; 
		case 5:
			strcpy(dia,"Viernes");
			break; 
		case 6:
			strcpy(dia,"Sabado");
			break;
		case 7:
			strcpy(dia,"Domingo");
			break;
		}
		
		printf("%d es %s\n",nroDia,dia);
		
		system("pause");
		return 0;
}

Es muy importante poner la sentencia break al finalizar el conjunto de acciones que se ejecutan dentro de cada caso ya que si la omitimos se ejecutarán secuencialmente todas las acciones de todos los casos subsiguientes.

Es decir, supongamos que el usuario ingresa el día número 5 y omitimos poner los breaks entonces el programa ingresará por case 5, asignará “Viernes” a dia, luego le asignará “Sábado” y luego “Domingo”. Por lo tanto, la salida será:

5 es Domingo

Para asignar el nombre de cada día a la variable dia, no utilizamos el operador de asignación, lo hacemos a través de la función strcpy. Esto lo explicaremos a continuación.

Asignación de valores alfanuméricos (función strcpy)

Como comentamos anteriormente las cadenas de caracteres tienen un tratamiento especial ya que en C se implementan sobre arrays (conjuntos) de caracteres.

Por este motivo, no podemos utilizar el operador de asignación = para asignarles valor. Tenemos que hacerlo a través de la función de biblioteca strcpy (definida en el archivo “string.h”) como vemos en las siguientes líneas de código:

// defino un "conjunto" de 10 variables de tipo char
char s[10];

// strcpy asigna cada uno de los caracteres de "Hola"
// a cada una de las variables del conjunto s
strcpy(s,"Hola");

Esta función toma cada uno de los caracteres de la cadena “Hola” y los asigna uno a uno a los elementos del conjunto s.

Gráficamente, podemos verlo así:

1. Definimos un array de 10 caracteres (o un conjunto de 10 variables de tipo char) char s[10];

2. Asignamos uno a uno los caracteres de la cadena “Hola” a los caracteres de s. strcpy(s, "Hola");

Como vemos strcpy asigna el i-ésimo carácter de la cadena “Hola” al i-ésimo carácter del conjunto o array s.

Además strcpy agrega el carácter especial '\0' (léase “barra cero”) que delimita el final de la cadena. Es decir que si bien s tiene espacio para almacenar 10 caracteres nosotros solo estamos utilizando 5. Cuatro para la cadena “Hola” más 1 para el '\0'.

Vale decir entonces que en un array de n caracteres podremos almacenar cadenas de, a lo sumo, n-1 caracteres ya que siempre se necesitará incluir el carácter de fin de cadena '\0' al final.

#include <stdio.h>
int main() {
	char nombre[] = "Pablo";
	int edad = 39;
	double altura = 1.70;

	printf("Mi nombre es %s, tengo %d anios y mido %lf metros.\n", nombre, edad, altura);
 
	system("pause");
	return 0;
}

Aquí utilizamos el operador de asignación = para asignar el valor “Pablo” a la variable nombre. Esto solo se puede hacer al momento de definir la variable.

Incluso, como no hemos dimensionado la cantidad de caracteres que el array nombre puede contener, C dimensionará el conjunto de caracteres con tantos elementos como sea necesario para mantener la cadena “Pablo” más 1 para contener el '\0'.

Es recomendable modificar el programa anterior de la siguiente manera:

#include <stdio.h>
int main() {
	char nombre[20];
	nombre = "Pablo";

	// :
	// todo lo demas...
	// :
	
	return 0;
} 

Aquí estamos intentando asignar “Pablo” a nombre, pero en una línea posterior a la declaración de la variable. Al compilar obtendremos el siguiente error:

datospersona.c: In function 'main':
datospersona.c:8: error: incompatible types in assignment

Estructura de repetición

La estructura de repetición, también llamada “estructura iterativa” o “ciclo de repetición”, permite ejecutar una y otra vez un conjunto de acciones en función de que se verifique una determinada condición lógica.

Según sea exacta o inexacta la cantidad de veces que el ciclo iterará podemos clasificar a la estructura de repetición de la siguiente manera:

• Estructura de repetición inexacta que itera entre 0 y n veces
• Estructura de repetición inexacta que itera entre 1 y n veces
• Estructura de repetición exacta que itera entre i y n veces, siendo i <= n

Estructuras de repetición inexactas

Bucle While y Do While

Llamamos así a las estructuras que iteran una cantidad variable de veces. En C estas estructuras son el ciclo while y el ciclo do-while y las representamos así:

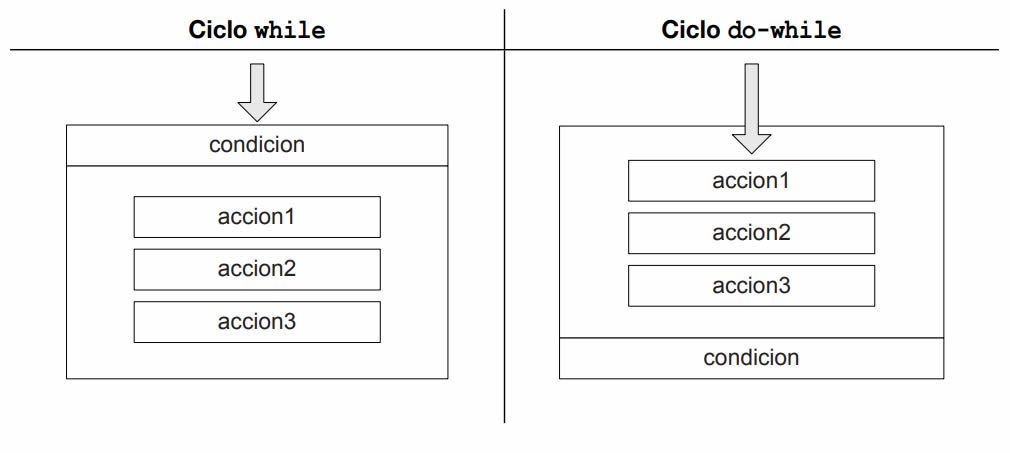
El ciclo while itera mientras que se cumpla la condición lógica indicada en su cabecera.

Si al llegar a esta estructura la condición resulta ser falsa entonces el ciclo no iterará ni siquiera una vez.

Por eso, decimos que se trata de un ciclo de repeticiones inexacto que puede iterar entre 0 y n veces. Además, como la condición se evalúa antes de ingresar al ciclo decimos que el while es un ciclo con “precondición”.

En cambio el bucle Do While:

La entrada al ciclo do-while no está condicionada, por lo tanto, las acciones encerradas dentro de esta estructura se realizarán al menos una vez.

Luego de esto se evaluará la condición lógica ubicada al pie de la estructura, que continuará iterando mientras que esta condición resulte verdadera.

En este caso, decimos que se trata de un ciclo de repeticiones inexacto que iterará entre 1 y n veces. El do-while es un ciclo con “poscondición”.

Problema 2.4

Se ingresa por teclado un conjunto de valores numéricos enteros positivos, se pide informar, por cada uno, si el valor ingresado es par o impar. Para indicar el final se ingresará un valor cero o negativo.

Análisis

Los datos de entrada de este problema son los números que ingresará el usuario. No sabemos cuántos números va a ingresar, solo sabemos que el ingreso de datos finalizará con la llegada de un valor cero o negativo.

Por esto, mientras que el número ingresado sea mayor que cero tenemos que “procesarlo” para indicar si es par o impar.

Para resolver este problema, utilizaremos un ciclo de repetición que iterará mientras que el número ingresado sea mayor que cero. Luego, dentro de la estructura lo procesaremos para determinar e informar si el número es par o impar.

Dentro del ciclo de repeticiones debe suceder “algo” que haga que, en algún momento, la condición lógica se deje de cumplir.

En este caso, por cada iteración volvemos a leer en la variable n el siguiente número del conjunto. Por lo tanto, cuando el usuario ingrese un valor cero o negativo la condición lógica resultará falsa y el ciclo dejará de iterar.

Notemos que si el conjunto de datos está vacío el usuario solo ingresará un valor cero o negativo con el que la condición del ciclo resultará falsa y, directamente, no ingresará. Veamos la codificación:

#include <stdio.h>
int main(){
	int n;
	printf("Ingrese un valor: ");
	scanf("%d",&n);

	while( n>0 ) {
		if( n%2 == 0 ) {
	 		printf("%d es par\n",n);
	 	} else {
	 		printf("%d es impar\n",n);
	 	}

	 	printf("Ingrese un valor: ");
		scanf("%d",&n);
	}
	
	system("pause");
	return 0;
}

Estructuras de repetición exactas

Bucle for

A diferencia de las estructuras inexactas, las estructuras exactas permiten controlar la cantidad de veces que van a iterar.

En general, se llaman “ciclos for” y definen una variable de control que toma valores sucesivos comenzando desde un valor inicial v_i y finalizando en un valor final v_n.

Así, el for itera exactamente v_n - v_i +1 veces y en cada iteración la variable de control tomará los valores v_i, v_i+1, v_i+2, ...,v_n

En C el ciclo for se implementa como una mezcla entre el “for tradicional” y el ciclo while. Gráficamente, lo representaremos así:

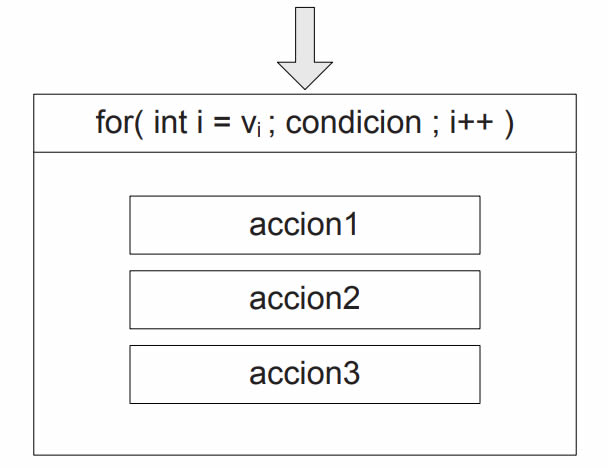
La cabecera del ciclo se compone de tres secciones separadas por ; (punto y coma).

En la primera sección, definimos la variable de control como una variable entera (en este caso es la variable i) y le asignamos un valor inicial.

En la segunda sección, definimos una condición lógica.

En la tercera sección, definimos la modalidad de incremento que se le aplicará a la variable de control. Con i++ le indicamos al for que en cada iteración incremente en 1 el valor de i.

El for iterará incrementando el valor de la variable i de uno en uno y mientras que se verifique dicha condición.

Es decir, si queremos que el ciclo itere exactamente n veces con una variable i variando entre 0 y n-1 tendremos que definir la cabecera del for de la siguiente manera:

for( int i=0; i<n; i++ )

Problema 2.5

Desarrollar un algoritmo que muestre por pantalla los primeros n números naturales considerando al 0 (cero) como primer número natural.

Análisis

El único dato de entrada que recibe el algoritmo es el valor n que el usuario deberá ingresar por teclado. Luego, la salida será: 0, 1, 2, ..., n-2, n-1. Es decir, si el usuario ingresa el valor 3 entonces la salida del algoritmo debe ser 0,1,2. Y si el usuario ingresa el valor 5 la salida será 0,1,2,3,4.

Para resolver el algoritmo utilizaremos una variable i cuyo valor inicial será 0.

Luego mostramos su valor y lo incrementamos para que pase a ser 1. Si repetimos esta operación mientras que i sea menor que n tendremos resuelto el problema.

Para simplificar la lectura de los diagramas, en algunos casos comenzaré a omitir los mensajes con indicaciones para el usuario. Por ejemplo, aquí decidí no incluir el mensaje “Ingrese un valor numérico”. Sin embargo, en la codificación sí los incluiré.

Como vemos, el for prácticamente resuelve todo el problema ya este ciclo define la variable i, le asigna el valor inicial 0, la incrementa de uno en uno e itera mientras que su valor sea menor que n. Dentro del for todo lo que queda por hacer es mostrar el valor de la variable i.

Veamos la codificación del algoritmo:

#include <stdio.h>
int main() {
	int n;

	printf("Ingrese un valor numerico: ");
	scanf("%d",&n);
	for(int i=0; i<n; i++) {
 		printf("%d\n",i);
 	}
	
	system("pause");
 	return 0;
}

Este problema también podemos resolverlo utilizando un ciclo while pero, entonces, la responsabilidad de incrementar la variable será nuestra. Para esto, en cada iteración luego de mostrar el valor de i incrementaremos su valor asignándole su valor actual “más 1”. En este caso, decimos que i es un contador.

Contadores

Definimos como contador a

A una variable cuyo valor iremos incrementando manualmente, de uno en uno, dentro de un ciclo de repetición.

Para incrementar el valor de una variable numérica, tenemos que asignarle “su valor actual más 1” de la siguiente manera:

// incrementamos el valor de la variable x
x = x+1;

La línea anterior debe leerse así: “a x le asigno x más 1”. Si el valor actual de x es 2, luego de incrementarlo su valor será 3. Los contadores siempre deben tener un valor inicial.

Resolveremos el problema anterior reemplazando el ciclo for por un ciclo while e incrementando manualmente un contador

Es muy importante asignarle un valor inicial a la variable que implementa el contador.

En el diagrama le asignamos el valor inicial 0 a la variable i. De no haberlo hecho entonces la condición del while no tendría sentido. Luego, al mostrar i estaríamos mostrando algo incierto. Tampoco podríamos asignarle a i “su valor actual más 1” porque i no tendría ningún valor actual.

Llamamos “inicializar” a la acción de asignarle valor inicial a una variable. Una variable que no está inicializada no tiene asignado ningún valor concreto. Es decir, no tiene valor.

Volviendo al diagrama inicializamos la variable i, pero no inicializamos la variable n.

Esto se debe a que n tomará su valor inicial luego de que el usuario lo ingrese por teclado.

Veamos la codificación:

#include <stdio.h>
int main() {
	int i, n;
	printf("Ingrese un valor numerico: ");
	scanf("%d",&n);
	i = 0;
	while( i<n ) {
 		printf("%d\n",i);
		i = i+1;
	}
	
	system("pause");
	return 0;
}

Acumuladores

Llamamos así a una variable cuyo valor iremos incrementando en cantidades variables dentro de un ciclo de repetición. Esto lo logramos de la siguiente manera:

x = x+n;

La diferencia entre un acumulador y un contador es que el contador se incrementa de a 1 en cambio el acumulador se incrementa de a n siendo n una variable. Obviamente, un contador es un caso particular de acumulador.

Problema 2.6

Determinar la sumatoria de los elementos de un conjunto de valores numéricos. Los números se ingresarán por teclado. Se ingresará un cero para finalizar.

Análisis

Para resolver este problema, utilizaremos un ciclo while dentro del cual acumularemos en la variable suma cada uno de los valores que ingrese el usuario. El ciclo de repetición iterará mientras que el valor ingresado sea distinto de cero.

La variable suma es un acumulador porque dentro del ciclo while su valor se incrementa de a n unidades siendo n un valor potencialmente distinto en cada iteración ya que toma cada uno de los valores que ingresa el usuario.

Seguimiento del algoritmo y “prueba de escritorio”

La prueba de escritorio es una herramienta que nos permite comprobar si el algoritmo realmente funciona como esperamos.

Básicamente, consiste en definir un conjunto de datos arbitrarios que llamaremos “lote de datos” y utilizarlos en un seguimiento, paso a paso, de cada una de las acciones del algoritmo controlando los valores que irán tomando las variables, las expresiones lógicas y la salida que se va a emitir.

Analizaremos una prueba de escritorio para el diagrama del problema anterior, considerando el siguiente lote de datos {5, 2, 3, 0}.

Comenzamos leyendo n que, según nuestro lote de datos, tomará el valor 5.

Inicializamos suma en 0 y luego entramos a un ciclo de repetición para iterar mientras que n sea distinto de 0 o, dicho de otro modo, mientras que la expresión “n es distinto de cero” sea verdadera.

Como n vale 5 se verifica la condición lógica e ingresamos al while. Dentro del while asignamos a suma su valor actual (cero) más el valor de n (cinco) por lo que ahora suma vale 5.

Luego volvemos a leer n que tomará el valor 2 y volvemos a la cabecera del ciclo de repetición para evaluar si corresponde iterar una vez más.

Como n (que vale 2) es distinto de cero volvemos a ingresar al while, asignamos a suma su valor actual (cinco) más el valor de n (dos) por lo que suma ahora vale 7.

Luego leemos n que tomará el valor 3. La condición del ciclo se sigue verificando porque n (que vale 3) es distinto de cero. Entonces asignamos a suma su valor actual (que es 7) más el valor de n (que es 3).

Ahora suma vale 10.

Volvemos a leer n que tomará el valor cero y evaluamos la condición del ciclo. Como la expresión “n es distinto de cero” resulta falsa el ciclo no volverá a iterar, salimos del while y mostramos el valor de la variable suma: 10.

Todo este análisis puede resumirse en la siguiente tabla que iremos llenando paso a paso, siguiendo el algoritmo y considerando que ingresan uno a uno los valores del lote de datos.

La tabla debe leerse de arriba hacia abajo y de izquierda a derecha. El lector puede acceder al videotutorial que muestra el desarrollo de esta misma prueba de escritorio.

Por último, veamos la codifi cación del algoritmo:

#include <stdio.h>
int main() {
	int n,suma;

	printf("Ingrese un valor numerico: ");
	scanf("%d",&n);
	suma=0;
	while( n!=0 ) {
		suma = suma+n;
		printf("Ingrese el siguiente valor: ");
		scanf("%d",&n);
	}

	printf("La suma es: %d\n",suma);
	
	system("pause");
	return 0;
}

El debugger, la herramienta de depuración

El debugger es una herramienta que permite seguir paso a paso la ejecución del código fuente del programa. También permite monitorear los valores que toman las variables y evaluar las expresiones.

Las IDE integran el debugger con el editor de código fuente de forma tal que, dentro del mismo editor, el programador pueda seguir línea por línea la ejecución del programa y así, depurarlo de errores de lógica.